非線形ダイナミクス

私たちの周りで起こっている出来事や自然界には複雑な現象が溢れています。 例としては、天気予報など長期的な予測は困難であるというようなことなどが挙げられます。 そのような複雑な現象は一見ランダムに見えても、実は背後に法則が存在することが多くあります。
その法則を科学するためには「非線形ダイナミクス」というものを考える必要があります。 そのような非線形なシステムで発生する現象の一つにカオス現象があります。

カオスとは何か？ 簡単に言えば、「未来の振る舞いを予測できない」ような現象です。 もう少し正確には「短期的振る舞いは厳密に決まるけれども、長期的未来の振る舞いは予測できない」ような現象です。
例えば、明日の天気のような短期的な振る舞いの予測はかなり正確に予測できても、数カ月先の天気、つまり長期的な振る舞いの予測は困難、事実上不可能と言えます。 これはつまり、初期値の僅かな違い（天気であれば気温や湿度の僅かな違い）が長期的には大きな変化（気温の僅かな差によって晴れるか雨が降るかが変わってしまう）を発生させるという事になります。

本研究室では、そのような従来の線形理論では説明できないような複雑な現象・問題を非線形ダイナミクスを用いたアプローチで解き明かす取り組みを行っています。

執筆: H26年度 M2 柳澤 健太郎

分岐現象

パワーエレクトロニクスのスイッチング電源のような非線形システムでは、入力の電圧や出力の抵抗、 コンデンサの容量などのパラメータを変化させることにより現れる現象が大きく変化することがしばしば起こります。 このような線形システムでは見られない大きな現象の変化は分岐現象と呼ばれます。 この分岐メカニズムが明らかにできると工学的にも多くの利点が生まれます。

例えば、「どのパラメータで所望の信号が取り出せるか」や「どのパラメータでシステムの安定性が変化するか」などがわかればシステム設計に活かすことができます。 本研究室では、様々な分岐を発生するモデルの合成と解析や、そのための理論構築やアルゴリズムの開発を行っています。

執筆: H26年度 M1 栗山 広宣

同期現象

同期現象とは"弱い相互作用による振動体のリズムの調和"のことです。 しかしこれではよくわかりませんよね。 つまり、"何らかの影響で複数の振動体が同じ振る舞いを起こす"ということです。 例としては、メトロノームの同期や蛍の同期的発光等があげられます。 このように同期現象は物理学や生物学などでも研究が行われています。

これはメトロノームの同期の例です。 つるされたすしおけの上にのせられたメトロノームは、はじめはバラバラな振る舞いをしていても時間が経つと同じ振る舞いをすることがわかります。 このような現象を"同相同期"と呼びます。

他にも同期にはいくつか種類があります。 同期現象の応用例としては、心臓のペースメーカーや通信信号の同期などがあげられます。 また、脳の神経の情報処理にも同期現象が確認されるので、将来の脳型コンピュータでは重要な役割を担うかもしれません。 本研究室ではこの同期現象を電気回路を用いて研究しています。

執筆: H26年度 B4 廣田 諒平

カオスとその応用

カオスの応用例の1つで通信やレーダーへ応用すると高い安全性や距離分解能が実現できるとの報告があります。 この応用を実現するためには高い周波数でカオス発生回路を動作させる必要があります。 その報告で用いられているカオス発生回路からは図1のようなカオス的振る舞いを観測できます。

しかし高い周波数では回路に内在する遅延の影響を無視することができなくなり、図2の様にシステムの軌道の振る舞いが変化します。 この状態ではカオスの性質が変わってしまいます。 そこで、回路に制御機構を加える事で高い周波数でも所望される振る舞いを実現できるカオス発生回路の開発に取り組んでいます。

執筆: H26年度 M2 西村 明日翔

最適化

最適化とは、「制約条件がある中で複数の選択肢を組み合わせ何らかの成果を出すとき、 その成果を最小、または最大にする」ことです。
乗り換え案内などでは、電車、バス、タクシーなどの複数の選択肢がある中で、 出発地点から目的地点までにかかる時間やお金、乗り換え回数などを最小化してくれるサービスであり、 まさに、移動ルートを最適化してくれるサービスです。

近年、システムの複雑化、大規模化に伴い、大規模システムに対する最適化問題において、 短い時間で高い精度の解を求めることが求められています。

Particle Swarm Optimization

Particle Swarm Optimization(PSO)は鳥や魚の群れの動きを最適化手法に応用したもので、 簡素なアルゴリズムで構成されることと、高い収束性を特徴とします。 PSOは電力配分問題やルーティング問題など、様々な問題に適用され、 その有効性が確認されています。

執筆: H26年度 M1 栗田 裕弥

その他

Cellular Automata (CA)

Cellular Automata (CA) は，非線形ダイナミクスで見られる複雑な現象のシミュレーションが可能です． CAは，セルと呼ばれる限られた状態を持つ構成要素を持ちます． セルはマス目のように区切られた離散的な空間の各位置に配置されます． 近くにあるセル同士は互いの状態から影響を受けて，セルの状態は変化していきます． このように，CAは局所的な相互作用をダイナミクスとして持ちます．

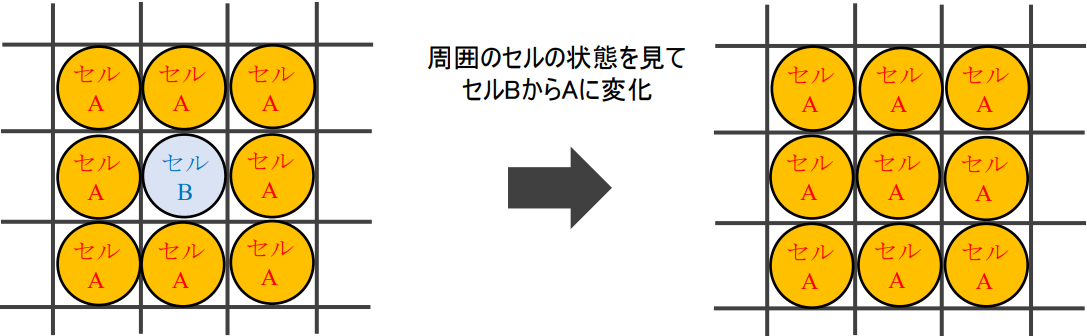
図1: CAの模式図．

本研究室ではCAを使った機械学習や生命系のパターン形成機構のモデル化を行っています． 下のアニメーションは本研究室で提案するモデル[1]を使った，パターン形成のシミュレーションです． ランダムにつくった状態を与えても徐々に秩序立てられ，やがてパターンを形成します．

図2: 本研究室の提案モデル[1]のパターン形成過程．

生命系を観察するにはそれなり設備がいりますが，CAはコンピュータ内で完結し，離散的でひとつひとつ起こっていることが観察しやすいという特徴があります． CAを使ってダイナミクスを観察することで，複雑な現象のメカニズムの理解に役立つと期待されます．

参考文献
[1] 長島 大晟, 坪根 正, 信学技報, vol. 123, no. 428, NLP2023-145, pp. 107-110, 2024 年.

執筆: R6年度 M2 長島大晟